Надстрочный и подстрочный текст

Надстрочный текст

Надстрочный текст в математике и физике применяется для обозначения векторов и углов между ними.

\vec{F}

\cos (\hat{a, b})

Надстрочный текст добавляется с помощью элемента <mover>, имеющего два дочерних элемента.

<mover>
  Выражение
  Надстрочный текст
</mover>

Первым идёт само выражение, а следующим за ним надстрочный текст. К примеру, написание вектора $\vec{AB}$ будет следующим.

Обратите внимание, что стрелка занимает всю ширину текста. Не все символы обладают способностью так растягиваться, и в браузере Chrome (а также в других браузерах на движке Blink) вид некоторых выражений будет отличаться от Firefox.

Рассмотрим следующий пример, где для обозначения угла между векторами в качестве надстрочного текста используется символ ^. Поскольку <mover> может содержать только два дочерних элемента, сгруппируем часть из них с помощью элемента <mrow>.

Результат данного примера в Firefox показан на рис. 1. Тот же пример в браузере Edge показан на рис. 2.

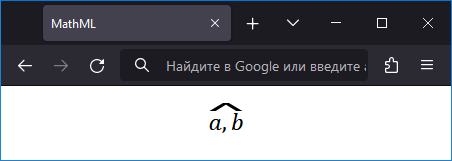
$Надстрочный текст в FIrefox$

Рис. 1. Надстрочный текст в FIrefox

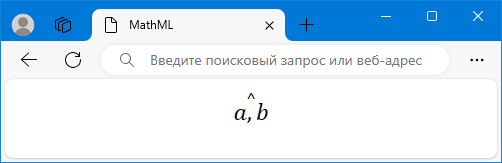
$Надстрочный текст в Edge$

Рис. 2. Надстрочный текст в Edge

Подстрочный текст

Подстрочный текст используется, в частности, для отображения пределов и математических супремумов.

\lim_{x \to ∞} \frac{1}{x} = 0

\sup_{k ⩾ 0} T^{(k)} (N)

Для создания подстрочного текста в MathML применяется элемент <munder>, который должен иметь два дочерних выражения.

<munder>
  Выражение
  Подстрочный текст
</munder>

Например, для отображения предела в качестве подстрочного текста воспользуемся элементом <mrow>, поскольку он позволяет группировать сразу несколько элементов (пример 1).

Пример 1. Использование <munder>

<!DOCTYPE html> <html lang="ru"> <head> <meta charset="utf-8"> <title>MathML</title> </head> <body> <math display="block"> <munder> <mi>lim</mi> <mrow> <mi>x</mi> <mo>→</mo> <mn>2</mn> </mrow> </munder> <mo fence="true" form="prefix" stretchy="false">(</mo> <mn>2</mn><mi>x</mi> <mo>+</mo><mn>1</mn> <mo fence="true" form="postfix" stretchy="false">)</mo> </math> </body> </html>

Надстрочный и подстрочный текст одновременно

Для отображения пределов интегрирования или границ суммирования применяется элемент <munderover>.

\int_{1}^{2} 2^{x} d x

\sum_{a}^{b} f (x) d x

\sum_{n = 1}^{5} n

Сам элемент содержит три обязательных дочерних элемента.

<munderover>
  Выражение
  Подстрочный текст
  Надстрочный текст
</munderover

Сперва пишется само выражение, затем идёт подстрочный текст и последним надстрочный текст. К примеру, пределы интегрирования от a до b запишутся так.

<munderover>
  <mo>∫</mo>
  <mi>a</mi>
  <mi>b</mi>
</munderover>

В примере 2 показано использование элемента <munderover> в комбинации с <mrow> для написания выражения с алгебраической суммой.

Пример 2. Использование <munderover>

<!DOCTYPE html> <html lang="ru"> <head> <meta charset="utf-8"> <title>MathML</title> </head> <body> <math display="block"> <msub> <mi>s</mi> <mi>n</mi> </msub> <mo>=</mo> <munderover> <mo>∑</mo> <mrow> <mi>i</mi><mo>=</mo><mn>1</mn> </mrow> <mi>n</mi> </munderover> <msub> <mi>m</mi> <mi>i</mi> </msub> <mi mathvariant="normal">Δ</mi> <msub> <mi>x</mi> <mi>i</mi> </msub> </math> </body> </html>

Итоги

Элемент <mover> применяется для написания надстрочного текста.
Элемент <munder> используется для отображения подстрочного текста.
Элемент <munderover> выводит надстрочный и подстрочный текст одновременно.

Перейти к заданиям

Автор: Влад Мержевич

Последнее изменение: 14.04.2025

Создайте выражение с помощью MathML, как показано на рис. 1.

Рис. 1

<!DOCTYPE html> <html lang="ru"> <head> <meta charset="utf-8"> <title>MathML</title> </head> <body> <p>Силы, с которыми две материальные точки воздействуют друг на друга, всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки. В виде формулы:</p> <math display="block"> <msub> <mover> <mi>F</mi> <mo>→</mo> </mover> <mn>1</mn> </msub> <mo>=</mo> <mo>−</mo> <msub> <mover> <mi>F</mi> <mo>→</mo> </mover> <mn>2</mn> </msub> </math> </body> </html>

Создайте выражение с помощью MathML, как показано на рис. 1.

Рис. 1

<!DOCTYPE html> <html lang="ru"> <head> <meta charset="utf-8"> <title>MathML</title> </head> <body> <p>Первый замечательный предел:</p> <math display="block"> <munder> <mi>lim</mi> <mrow> <mi>x</mi> <mo>→</mo> <mn>∞</mn> </mrow> </munder> <mfrac> <mrow> <mi>sin</mi> <mi>x</mi> </mrow> <mi>x</mi> </mfrac> <mo>=</mo> <mn>1</mn> <mtext>.</mtext> </math> </body> </html>

Создайте выражение с помощью MathML, как показано на рис. 1.

Рис. 1

<!DOCTYPE html> <html lang="ru"> <head> <meta charset="utf-8"> <title>MathML</title> <style> @font-face { font-family: XITSMath; src: url('/example/font/XITSMath-Regular.woff2'); } math { font-family: XITSMath; } </style> </head> <body> <p>Второй замечательный предел:</p> <math display="block"> <munder> <mi>lim</mi> <mrow> <mi>x</mi> <mo>→</mo> <mn>∞</mn> </mrow> </munder> <msup> <mrow> <mo fence="true" form="prefix">(</mo> <mn>1</mn> <mo>+</mo> <mfrac> <mn>1</mn> <mi>x</mi> </mfrac> <mo fence="true" form="postfix">)</mo> </mrow> <mi>x</mi> </msup> <mo>=</mo> <mi>e</mi> <mtext>.</mtext> </math> </body> </html>

Создайте выражение с помощью MathML, как показано на рис. 1.

Рис. 1

<!DOCTYPE html> <html lang="ru"> <head> <meta charset="utf-8"> <title>MathML</title> <style> @font-face { font-family: STIXTwoMath; src: url('/example/font/STIXTwoMath-Regular.woff2'); } math { font-family: STIXTwoMath; } </style> </head> <body> <p>Если функция f(x) непрерывна на промежутке [a, b] и F(x) некоторая первообразная функции f(x), то</p> <math display="block"> <munderover> <mo>∫</mo> <mi>a</mi> <mi>b</mi> </munderover> <mi>f</mi> <mo fence="true" form="prefix" stretchy="false">(</mo> <mi>x</mi> <mo fence="true" form="postfix" stretchy="false">)</mo> <mi>d</mi><mi>x</mi> <mo>=</mo> <mi>F</mi> <mo fence="true" form="prefix" stretchy="false">(</mo> <mi>b</mi> <mo fence="true" form="postfix" stretchy="false">)</mo> <mo>−</mo> <mi>F</mi> <mo fence="true" form="prefix" stretchy="false">(</mo> <mi>a</mi> <mo fence="true" form="postfix" stretchy="false">)</mo> <mtext>.</mtext> </math> </body> </html>

См. также

Рецепты

Как написать интеграл?

Как написать математическую сумму?