Извлечение корня

Квадратный корень — это операция, обратная возведению в квадрат, иными словами, когда число умножается на само себя.

a=x·x=x2 ⇔x=a

Например, квадратный корень из 9 равен 3, потому что 3 в квадрате равно 9.

32=9; 9=3

В MathML для написания квадратного корня применяется элемент <msqrt>, у которого должен быть только один дочерний элемент.

<msqrt>
  Выражение
</msqrt>

К примеру, корень из числа 16 запишется следующим образом.

<msqrt>
  <mn>16</mn>
</msqrt>

Сложные подкоренные выражения помещаются в элемент <mrow>. В примере 1 показана формула решения квадратного уравнения.

Пример 1. Использование <msqrt>

<!DOCTYPE html> <html lang="ru"> <head> <meta charset="utf-8"> <title>MathML</title> </head> <body> <math display="block"> <msub> <mi>x</mi> <mn>1,2</mn> </msub> <mo>=</mo> <mfrac> <mrow> <mo>−</mo> <mi>b</mi> <mo>±</mo> <msqrt> <mrow> <msup> <mi>b</mi> <mn>2</mn> </msup> <mo>−</mo> <mn>4</mn> <mi>a</mi> <mi>c</mi> </mrow> </msqrt> </mrow> <mrow> <mn>2</mn> <mi>a</mi> </mrow> </mfrac> </math> </body> </html>

Знак корня

Браузеры достаточно корректно отображают знак корня, но небольшие отличия могут наблюдаться в разных браузерах и операционных системах. Это зависит от шрифта, используемого для отображения математических знаков, а также от масштаба веб-страницы. На рис. 1 показан вид квадратного корня в браузере Firefox. Тот же корень в браузере Edge показан на рис. 2.

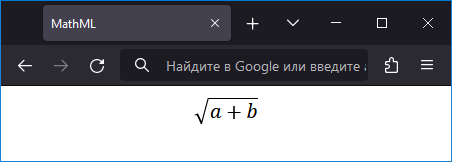
Корень в Firefox

Рис. 1. Корень в Firefox

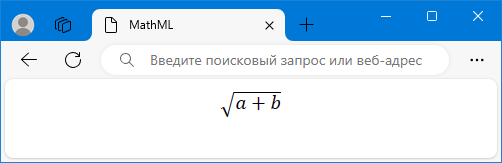
Корень в Edge

Рис. 2. Корень в Edge

Если такие отличия неприемлемы и требуется единообразие в разных браузерах, то для элемента <math> можно установить специальный шрифт через @font-face. Список доступных математических шрифтов, подходящих для работы MathML, можно найти на этом сайте.

trac.webkit.org/wiki/MathML/Fonts

После скачивания файла шрифта, он подключается следующим образом (пример 2).

Пример 2. Математический шрифт

<!DOCTYPE html> <html lang="ru"> <head> <meta charset="utf-8"> <title>MathML</title> <style> @font-face { font-family: XITSMath; src: url('/example/font/XITSMath-Regular.woff'); } math { font-family: XITSMath; } </style> </head> <body> <math display="block"> <msqrt> <mrow> <mi>a</mi> <mo>+</mo> <mi>b</mi> </mrow> </msqrt> </math> </body> </html>

Корень n-й степени

Если в математическом выражении требуется не квадратный корень, а кубический или корень произвольной степени, то в MathML используется элемент <mroot>. У него два дочерних элемента.

<mroot>
  Выражение
  Степень корня
</mroot>

Сперва идёт подкоренное выражение, затем степень корня. К примеру, для написания кубического корня из Z, запись будет следующая.

<mroot>
  <mi>Z</mi>
  <mn>3</mn>
</mroot>

Опять же, сложные выражения группируются с помощью элемента <mrow>, как это показано в примере 3.

Пример 3. Использование <mroot>

<!DOCTYPE html> <html lang="ru"> <head> <meta charset="utf-8"> <title>MathML</title> </head> <body> <p>Свойство корня:</p> <math display="block"> <mroot> <mi>a</mi> <mn>n</mn> </mroot> <mo>·</mo> <mroot> <mi>b</mi> <mn>n</mn> </mroot> <mo>=</mo> <mroot> <mrow> <mi>a</mi> <mo>·</mo> <mi>b</mi> </mrow> <mn>n</mn> </mroot> </math> </body> </html>

Итоги

  • Элемент <msqrt> используется для написания квадратного корня.
  • Элемент <mroot> применяется для написания корня произвольной степени.

Перейти к заданиям

Автор: Влад Мержевич
Последнее изменение: 14.04.2025

Создайте выражение с помощью MathML, как показано на рис. 1.

Рис. 1

<!DOCTYPE html> <html lang="ru"> <head> <meta charset="utf-8"> <title>MathML</title> <style> @font-face { font-family: XITSMath; src: url('/example/font/XITSMath-Regular.woff'); } math { font-family: XITSMath; } </style> </head> <body> <p>В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.</p> <math display="block"> <mi>c</mi> <mo>=</mo> <msqrt> <mrow> <msup> <mi>a</mi> <mn>2</mn> </msup> <mo>+</mo> <msup> <mi>b</mi> <mn>2</mn> </msup> </mrow> </msqrt> </math> </body> </html>

Создайте выражение с помощью MathML, как показано на рис. 1.

Рис. 1

<!DOCTYPE html> <html lang="ru"> <head> <meta charset="utf-8"> <title>MathML</title> </head> <body> <p>Решите уравнение:</p> <math display="block"> <msqrt> <mrow> <mi>x</mi> <mo>+</mo> <mn>3</mn> </mrow> </msqrt> <mo>=</mo> <mroot> <mrow> <mn>4</mn> <mi>x</mi> <mo>+</mo> <mn>12</mn> </mrow> <mn>3</mn> </mroot> </math> </body> </html>

Создайте выражение с помощью MathML, как показано на рис. 1.

Рис. 1

<!DOCTYPE html> <html lang="ru"> <head> <meta charset="utf-8"> <title>MathML</title> <style> @font-face { font-family: XITSMath; src: url('/example/font/XITSMath-Regular.woff'); } math { font-family: XITSMath; } </style> </head> <body> <p>Первая космическая скорость:</p> <math display="block"> <msub> <mi>v</mi> <mn>1</mn> </msub> <mo>=</mo> <msqrt> <mrow> <mi>G</mi> <mfrac> <mi>M</mi> <mi>R</mi> </mfrac> </mrow> </msqrt> <mtext>,</mtext> </math> <p>где G — гравитационная постоянная, M — масса планеты, R — радиус орбиты.</p> </body> </html>